Figure 1: A curved path $C$ from $A$ to $B$.

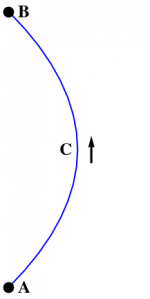
The Fundamental Theorem of Calculus is about integrating the derivative of a function along a curve, namely: \begin{equation} \int_C df = \int_{\partial C} f = f\Big|_A^B \end{equation} where the curve $C$ starts at point $A$ and ends at point $B$, as shown in Figure 1. This theorem includes both the single-variable statement that \begin{equation} \int_a^b \frac{df}{dx} \>dx = f(b)-f(a) \end{equation} in which case the curve lies along the $x$-axis, but also the Fundamental Theorem for Gradient, namely \begin{equation} \int_C \grad f\cdot d\rr = f\Big|_A^B \end{equation} along any smooth curve $C$.

Green's Theorem is about integrating vector fields in the plane. If $F=F_x\,dx+F_y\,dy$, then \begin{equation} dF = \left( \Partial{F_y}{x} - \Partial{F_x}{y} \right) \> dx\wedge dy \end{equation} so that \begin{equation} \int_S dF = \int_{\partial S}F \Longrightarrow \int_S \left( \Partial{F_y}{x} - \Partial{F_x}{y} \right) \> dA = \oint_{\partial S} F_x\,dx+F_y\,dy \end{equation} which is the special case of Stokes' Theorem restricted to the plane.

Figure 2: The geometry of Stokes' Theorem: The surface $S$ is a three-dimensional “butterfly net”; the curve $\partial S$ is its rim.

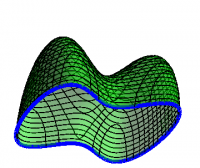
Stokes' Theorem is about integrating the curl of a vector field. If $F=\FF\cdot d\rr$, then \begin{equation} dF = *({*}dF) = \grad\times\FF\cdot d\AA \end{equation} so that \begin{equation} \int_S dF = \int_{\partial S}F \Longrightarrow \int_S \grad\times\FF\cdot d\AA = \oint_{\partial S} \FF\cdot d\rr \end{equation} The surface $S$ and its boundary $\partial S$ are shown in Figure 2.

Figure 3: The geometry of the Divergence Theorem: The surface $\partial R$ is the dumbbell-shaped surface shown; the region $R$ is its interior.

The Divergence Theorem is about integrating the divergence of a vector field. If $F=\FF\cdot d\rr$, then \begin{align} {*}F &= \FF\cdot d\AA \\ d{*}F &= *({*}d{*}F) = \grad\cdot\FF \>dV \\ \end{align} so that \begin{equation} \int_R d{*}F = \int_{\partial R}{*}F \Longrightarrow \int_R \grad\cdot\FF \>dV = \oint_{\partial R} \FF\cdot d\AA \end{equation} The region $R$ and its boundary $\partial R$ are shown in Figure 3.