In any dimension and signature, it turns out there is a unique (local) geometry of constant (sectional) curvature, which can be classified by the value of the scalar curvature $R$. These three possibilities are illustrated for two dimensions with Euclidean signature in Figure 1, showing a plane (zero curvature), sphere (constant positive curvature), and Lorentzian hyperboloid (constant negative curvature), respectively. In each case, the surface is two-dimensional, even though the representation shown is embedded in three dimensions. Furthermore, the hyperboloid is a Riemannian surface (its metric is positive-definite), even though it is shown embedded in three-dimensional Minkowski space. An isometric representation does exist in three-dimensional Euclidean space, namely the pseudosphere 1) but the analogy to the sphere is less apparent in this representation.

 
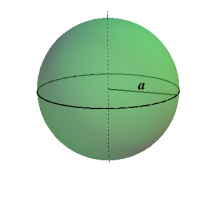
Figure 1: The two-dimensional surfaces of constant curvature, namely the plane, the sphere, and the (Lorentzian) hyperboloid.

We consider here the case of three-dimensional surfaces with Euclidean signature, which can also be represented as in Figure 1, but with one dimension suppressed.

Zero Curvature

If $R=0$, then the geometry is flat; this is ordinary Euclidean space. The line element can be brought to the form \begin{align} ds^2 &= dx^2 + dy^2 + dz^2 \nonumber\\ &= dr^2 + r^2 \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \nonumber\\ &= d\psi^2 + \psi^2 \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \end{align} where $r=\psi$. This geometry is just (Euclidean) $\RR^3$.

Positive Curvature

If $R=6/a^2>0$, then the geometry is spherical. The line element can be brought to the form \begin{align} ds^2 &= a^2 \left( d\psi^2 + \sin^2\psi \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \right) \nonumber\\ &= a^2 \left( \frac{dr^2}{1-r^2} + r^2 \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \right) \end{align} where $r=\sin\psi$. We can embed this surface in Euclidean $\RR^4$ with coordinates ($w$,$x$,$y$,$z$) as the set of points satisfying \begin{equation} w^2 + x^2 + y^2 + z^2 = a^2 \end{equation}

Negative Curvature

If $R=-6/a^2<0$, then the geometry is hyperbolic. The line element can be brought to the form \begin{align} ds^2 &= a^2 \left( d\psi^2 + \sinh^2\psi \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \right) \nonumber\\ &= a^2 \left( \frac{dr^2}{1+r^2} + r^2 \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \right) \end{align} where $r=\sinh\psi$. We can embed this surface in Minkowskian $\RR^4$ with coordinates ($T$,$x$,$y$,$z$) as the set of points satisfying \begin{equation} T^2 - x^2 - y^2 - z^2 = a^2 \end{equation}

All three cases can be written simultaneously as \begin{equation} ds^2 = a^2 \left( \frac{dr^2}{1-kr^2} + r^2 \left( d\theta^2 + \sin^2\theta\,d\phi^2 \right) \right) \end{equation} where $k=a^2 R/6\in\{-1,0,1\}$. (The value of $a$ corresponds to an irrelevant scale if $R=0$.)