A pion of (rest) mass $m$ and (relativistic) momentum $p={3\over4}mc$ decays into 2 (massless) photons. One photon travels in the same direction as the original pion, and the other travels in the opposite direction. Find the energy of each photon.

First solution: We begin by determining the energy and momentum of the pion. Since $p=\frac34mc$, we have immediately that \begin{equation} \sinh\beta = \frac{p}{mc} = \frac34 \end{equation} from which it follows that \begin{equation} \cosh\beta = \frac54 \end{equation} by simple (hyperbolic) triangle trigonometry. Thus, the total energy is given by \begin{equation} E = mc^2\cosh\beta = \frac54\,mc^2 \end{equation} Since each photon satisfies $E_i=|p_i|c$, and since without loss of generality we can assume $p_1>0$ and $p_2<0$, conservation of energy-momentum tells us that \begin{eqnarray} E_1 - E_2 &=& pc = \frac34\,mc^2 \\ E_1 + E_2 &=& E = \frac54\,mc^2 \end{eqnarray} from which it follows immediately that \begin{eqnarray} E_1 &=& mc^2 \\ E_2 &=& \frac{mc^2}{4} \end{eqnarray}

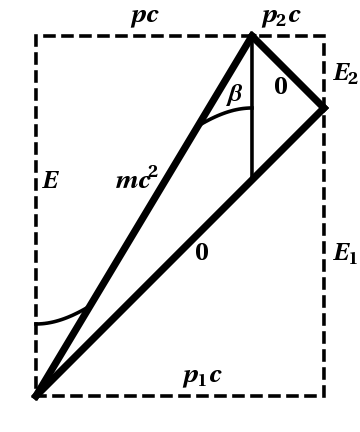Figure 10.3: Momentum diagram for the decay of a pion into photons.

Second solution: Use a momentum diagram, as shown in Figure 10.3. The computation is the same as before.

 
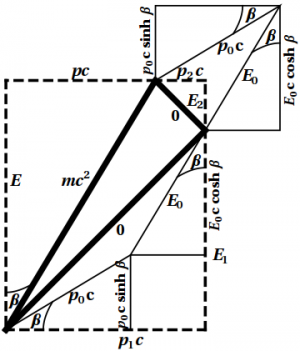
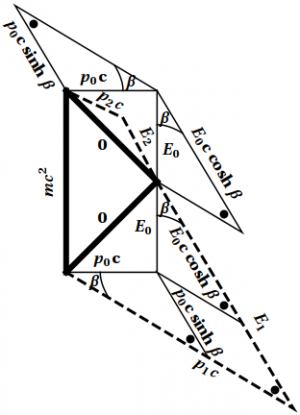
Figure 10.4: Analyzing pion decay using hyperbola geometry.

Third solution: Use hyperbola geometry and triangle trigonometry, as shown in Figure 10.4 in both the given reference frame and that of the pion, taking advantage of the fact that, in the center-of-mass frame (the rest frame of the pion), the two photons must have the same energy $E_0$ and equal but opposite momenta $\pm p_0c=\pm E_0$. The details are left to the reader.