Chapter 1: Introduction
- §1. Line Elements
- §2. Circle Trig
- §3. Hyperbola Trig
- §4. Geometry of SR
- §5. Differential Forms
- §6. Geodesics
- §7. The Physics of GR
Circle Trig
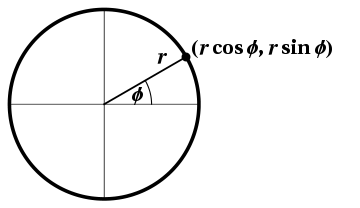 Figure 1: Defining the (circular) trigonometric functions via a circle.
Figure 1: Defining the (circular) trigonometric functions via a circle.
What is the fundamental idea in trigonometry? Although often introduced as the study of triangles, trigonometry is really the study of circles.
One way to construct the trigonometric functions is as follows:
- Draw a circle of radius $r$, that is, the set of points at constant distance $r$ from the origin.
- Measure arclength $s$ along the circle by integrating the (square root of the) line element.
- Define angle measure as $\phi=s/r$.
- Assuming an angle in standard position (counterclockwise from the positive $x$-axis), define the coordinates of the (other) point where the sides of the angle meet the given circle to be $(r\cos\phi,r\sin\phi)$, as shown in Figure 1.
Notice the key role that arclength plays in this construction. To measure an angle, and hence to define the trigonometric functions, one must know how to measure arclength. 1)
See Circle Geometry for further details.
1)
This is not as easy as it sounds. It is straightforward to use $x^2+y^2=r^2$
to obtain $x\,dx+y\,dy=0$, so that $ds^2=r^2\,dy^2/x^2$. But it is not
obvious how to integrate $ds$ without using a trig substitution! This can
however be done, since a little algebra shows that
\[
i \, d\phi
= \frac{i}{r} \> ds
= \frac{i\,dy}{x} \, \frac{1+i\frac{y}{x}}{1+i\frac{y}{x}}
= \frac{d(x+iy)}{x+iy}
\]
which leads to Euler's formula
\[
r \, e^{i\phi} = x + iy
\]
relating the sine and cosine functions to the complex exponential function,
and expressing arclength in terms of the complex logarithm function. Power
series expansions can now be used to determine arclength as a function of
position, and to provide expressions for the trigonometric functions in terms
of their argument. Yes, one could instead simply define $\pi$ as usual as the
ratio of circumference to diameter, but that construction does not generalize
to other geometries.