- §1. The Rindler Metric
- §2. Rindler Geometry
- §3. Rindler Geodesics
- §4. Extending Rindler
The Rindler Metric
We digress briefly from our discussion of the Schwarzschild geometry in order to consider a much simpler geometry with many of the same properties.
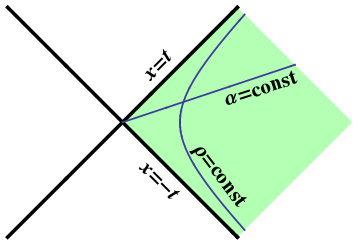 Figure 1: The shaded region is the Rindler wedge in Minkowski space, which
is covered by the Rindler coordinates ($\rho$,$\alpha$).
Figure 1: The shaded region is the Rindler wedge in Minkowski space, which
is covered by the Rindler coordinates ($\rho$,$\alpha$).
Consider two-dimensional Minkowski space, with line element \begin{equation} ds^2 = -dt^2 + dx^2 \end{equation} and introduce hyperbolic polar coordinates $(\rho,\alpha)$ via \begin{align} x &= \rho\,\cosh\alpha \\ t &= \rho\,\sinh\alpha \end{align} so that we have \begin{align} \rho^2 &= x^2 - t^2 \\ \tanh\alpha &= \frac{t}{x} \end{align} Using these coordinates, the line element becomes \begin{equation} ds^2 = d\rho^2 - \rho^2\,d\alpha^2 \end{equation} which is called the Rindler metric; the coordinates $(\rho,\alpha)$ are also called Rindler coordinates.
Since $\rho$ appears to be a sort of radial coordinate, and since this line element is degenerate at $\rho=0$, we will assume $\rho>0$; there are no restrictions on $\alpha$. With these assumptions, Rindler coordinates only cover the part of Minkowski space satisfying $x>|t|$, as shown in Figure 1.