- §1. The Rindler Metric
- §2. Rindler Geometry
- §3. Rindler Geodesics
- §4. Extending Rindler
Rindler Geodesics
Taking the “square root” of the line element, we have \begin{equation} d\rr = \rho\,d\alpha\,\Ahat + d\rho\,\Rhat \end{equation} where \begin{align} \Ahat\cdot\Ahat &= -1 \\ \Rhat\cdot\Rhat &= 1 \\ \Ahat\cdot\Rhat &= 0 \end{align} Since the line element depends only on $\rho$, but not on $\alpha$, there is a Killing vector 1) \begin{equation} \Avec = \rho\,\Ahat \end{equation} since \begin{equation} \Avec\cdot\grad f = \Partial{f}{\alpha} \end{equation} (and of course $\grad f\cdot d\rr=df$). Thus, there is one constant of the motion, namely \begin{equation} e = -\Avec\cdot\vv = \rho^2\dot\alpha \end{equation} since \begin{equation} \vv = \dot{\rr} = \rho\,\dot\alpha\,\Ahat + \dot\rho\,\Rhat \end{equation} Since the two-velocity $\vv$ is always a unit vector, we also have \begin{equation} -\rho^2\,\dot\alpha^2 + \dot\rho^2 = -1 \end{equation} which brings the geodesic equation to the form \begin{align} \dot\alpha &= \frac{e}{\rho^2} \\ \dot\rho^2 &= \frac{e^2}{\rho^2} -1 \end{align}
What does the constant $e$ represent? Suppose that $e=1$. Then $\dot\rho=0$ when $\rho=1$. Thus, as with radial geodesics in the Schwarzschild geometry, $e$ determines the maximum “radius” $\rho$ attained by an object moving along a given geodesic.
Notice that in Rindler coordinates \begin{equation} \frac{d\rho}{d\alpha} = \frac{\dot\rho}{\dot\alpha} = -\frac{\sqrt{e^2/\rho^2-1}}{e/\rho^2} = -\frac{\rho\sqrt{e^2-\rho^2}}{e} \end{equation} along a geodesic, and that this expression approaches $0$ as $\rho$ approaches $0$. Thus, a single Rindler observer at fixed $\rho$, for whom $\alpha$ is (proportional to) proper time, “sees” the object stop at $\rho=0$. On the other hand, the speed of the object is surely better described as the ratio of “Rindler distance” $d\rho$ to “Rindler time” $\rho\,d\alpha$, namely \begin{equation} \frac{d\rho}{\rho\,d\alpha} = -\frac{\sqrt{e^2-\rho^2}}{e} \label{rvel} \end{equation} which approaches $-1$ as $\rho$ approaches $0$. According to this interpretation, the object is moving at the speed of light at $\rho=0$!
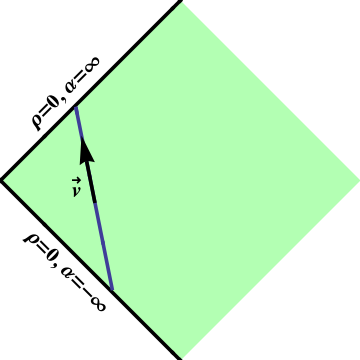 Figure 1: Rindler geodesics are straight lines in Minkowski space.
Figure 1: Rindler geodesics are straight lines in Minkowski space.
Which of these interpretations is correct? Neither! We know that the geodesics in Minkowski space are straight lines, such as the one shown in Figure 1. An object moving along a straight line in Minkowski space will cross the line $\rho=0$, which is just $x=\pm t$, at the same constant speed it started with.
How is this possible? A straight line approaching the future boundary ($x=t$), as shown in Figure 1, rapidly approaches $\alpha=\infty$, so it is no wonder that $\frac{d\rho}{d\alpha}$ approaches $0$. And (\ref{rvel}) gives the relative speed between the object and a Rindler observer; it is the latter, not the former, that approaches the speed of light.
This example shows that the problems in the description of geodesic motion near $\rho=0$ lie entirely with the choice of Rindler coordinates; the problems would go away if we would only switch back to Minkowski coordinates. But is there a way to see this within Rindler geometry? We address this question in the next section.